Delphi 3. Библиотека программиста
Пропавшая функция Poly
При подготовке полного списка функций модуля Math, приведенного в конце главы, я намеренно пропустил одну из функций. Почему? Потому что фирма Borland тоже не документировала ее! Непонятно, должна эта функция присутствовать в модуле Math или нет. Более того, найти ее можно только при просмотре исходного текста модуля Math во время подготовки главы для этой книги…
Что же делает эта загадочная функция? Выглядит она так:
function Poly(X: Extended; const Coefficients: array of Double):
Extended;
Функция Poly предназначена для вычисления полиномов. Единственное ограничение состоит в том, что это должны быть полиномы лишь одной переменной. Функция Poly получает переменную X, для которой вычисляется полином, и массив коэффициентов. Коэффициенты должны быть упорядочены по возрастанию степеней X.
Следовательно, для следующего полинома:
4x4 [+ 0x3] _ x2 + 3x + 34
массив коэффициентов должен быть упорядочен так:
34, 3, _1, 0, 4
Если бы вам потребовалось снабдить функцию Poly пользовательским интерфейсом, вероятно, получилось бы что-то наподобие программы PolyProject (см. рис.11.2).
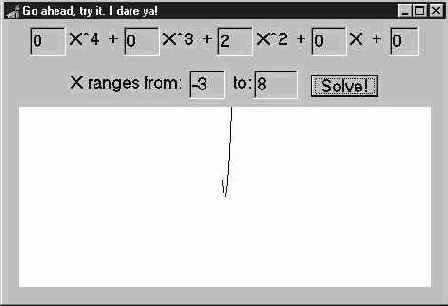
Рис. 11.2. Графическое представление
Программа PolyProject (она находится на CD-ROM в подкаталоге этой главы) как раз и является таким интерфейсным приложением. Она позволяет задать полином, а затем выводит его график. Обратите внимание — в главном окне программы PolyProject наряду с надписями имеется несколько текстовых полей для ввода коэффициентов полинома. Однако вся основная работа PolyProject выполняется в обработчике события OnClick кнопки Solve!:
procedure TForm1.SolveButtonClick(Sender: TObject); var i : Integer; XCoes : array[0..4] of double; X,Y, OffsetX, OffsetY : Integer; NewRect: TRect;Прежде всего мы заполняем массив XCoes введенными значениями коэффициентов:
begin XCoes[0] := StrToFloat(TxtX0.Text); XCoes[1] := StrToFloat(TxtX1.Text); XCoes[2] := StrToFloat(TxtX2.Text); XCoes[3] := StrToFloat(TxtX3.Text); XCoes[4] := StrToFloat(Tx1tX4.Text);После этого необходимо задать начало координат для построения графика. Обычно я использую центр элемента TImage, но при желании можно выбрать любую другую точку:
OffsetX := Image1.Width div 2; OffsetY := Image1.Height div 2;Затем мы инициализируем координату X и очищаем график, заполняя Image1 сплошным белым прямоугольником. Присваивание соответствующего значения свойству Image1.Canvas.Brush.Color гарантирует, что график будет выводиться черным цветом:
X := 0; { Для надежности инициализируем X }
NewRect := Rect(0, 0, Image1.Width, Image1.Height);
Image1.Canvas.Brush.Color := clWhite;
Image1.Canvas.FillRect(NewRect);
Image1.Canvas.Brush.Color := clBlack;
Пора заняться вычислениями. Сначала мы определяем положение начальной точки графика. До входа в цикл for мы ничего не рисуем, просто перед любым серьезным рисованием необходимо установить «перо» в исходную позицию. Затем мы вызываем функцию Poly, передавая ей значение из текстового поля с нижней границей диапазона (TxtRangeStart) и массив XCoes:
with Image1.Canvas do begin Y := Trunc(Poly(StrToInt(TxtRangeStart.Text), XCoes)); ...Возможно, вы удивитесь тому, что я округляю результат функции Poly. Это делается исключительно для рисования: функция Poly возвращает значение с плавающей точкой (тип Extended), а Windows API работает только с целыми координатами.
Полученный результат преобразуется в пару (X, Y), которая соответствует нашей центральной точке, после чего «перо» перемещается в эту точку:
X := StrToInt(TxtRangeStart.Text) + OffsetX; Y := OffsetY - Y; MoveTo(X,Y);Затем мы перебираем значения X из заданного интервала, начиная с нижней границы +1 (я только что упоминал о нижней границе) и вплоть до значения верхней границы из соответствующего текстового поля (TxtRangeEnd):
for i := StrToInt(TxtRangeStart.Text) + 1 to StrToInt(TxtRangeEnd.Text) do begin Y := Trunc(Poly(I, XCoes)); X := I + OffsetX; Y := OffsetY - Y; LineTo(X,Y); MoveTo(X,Y); end;Хотя функция Poly является единственной общедоступной , но недокумен тированной функцией модуля Math, в секции implementation можно найти еще несколько интересных процедур (одна из них, например, определяет, является ли величина A «бесконечно малой» по отношению к B!). Ограниченный объем главы не позволяет мне рассказать о них подробнее, но я бы порекомендовал изучить эти функции, если у вас есть исходные тексты и, конечно, терпение!
То, чего не было в Паскале
В модуле Math появилось то, чего никогда не было в Паскале — «официаль ная» функция для возведения в степень. Более того, модуль Math содержит сразу две такие функции.
Первая из них, Power, получает два параметра типа Extended — основание и показатель степени. Вторая функция, IntPower, получает один параметр типа Extended (основание) и один целый параметр (показатель степени).
Отличия между ними заключаются в том, что функция IntPower, как и многие функции модуля Math, написана целиком на оптимизированном ассемблере для работы с Pentium FPU, что делает ее достаточно быстрой.
Если вы не знаете, какую функцию следует использовать в вашем приложении, не огорчайтесь.
Хотя это нигде не объясняется и не документируется, функция Power сама определяет, является ли показатель степени целым числом. Если это так, Power вызывает IntPower. Если же показатель является числом с плавающей точкой, Power вычисляет результат каноническим способом, через натуральный логарифм и экспоненту.
